AVL Bäume
Leider verliert durch "ungeschicktes" Einfügen ein binärer Suchbäumen manchmal seine positiven Eigenschaften. Um dies zu verhindern ist die Idee eines ausbalancierten binären Suchbaums entstanden - einem sogenannten AVL () Baum.
Der AVL-Baum ist nach den sowjetischen Mathematikern Georgi Maximowitsch Adelson-Velski und Jewgeni Michailowitsch Landis benannt, die die Datenstruktur im Jahr 1962 vorstellten. Damit ist der AVL-Baum die älteste Datenstruktur für balancierte Bäume.
Er bildet eine Datenstruktur in der Informatik in Form eines binären Suchbaums mit der zusätzlichen Eigenschaft, dass sich an jedem Knoten die Höhe der beiden Teilbäume um höchstens eins unterscheidet.[2] Diese Eigenschaft lässt seine Höhe nur logarithmisch mit der Zahl der Schlüssel wachsen und macht ihn zu einem balancierten binären Suchbaum. Die maximale (und mittlere) Anzahl der Schritte (Vergleiche), die nötig sind, um An- oder Abwesenheit eines Schlüssels festzustellen, hängt direkt mit der Höhe zusammen. Ferner ist der maximale Aufwand für Operationen zum Einfügen und Entfernen eines Schlüssels proportional zur Höhe des Baums und damit ebenfalls logarithmisch in der Zahl der Schlüssel; der mittlere Aufwand ist sogar konstant, wenn das Positionieren auf das Zielelement nicht mitgerechnet wird.
Viele Operationen, insbesondere die Navigationsoperationen, sind direkt von den binären Suchbäumen zu übernehmen. Bei den modifizierenden Operationen muss jedoch das AVL-Kriterium beobachtet werden, womit auf jeden Fall kleine Anpassungen durchzuführen sind, die bis zu Höhenkorrekturen durch sogenannte Rotationen reichen können. (Quelle: https://de.wikipedia.org/wiki/AVL-Baum)
Aufgaben
- Macht euch mit Hilfe des Videos mit den Möglichkeiten eines AVL Baumes vertraut und bereitet euch darauf vor die Fachbegriffe (Balancefaktor, Rotation, Doppelrotaion usw.) zu erläutern.
- Zeichnen den binären Suchbaum, der entsteht, wenn in einen leeren binären Suchbaum die folgenden Werte eingefügt werden: 100, 90, 80, 70, 60, 50, 40, 30, 20
flowchart TD
A(("100")) --> B(("90"))
B --> C(("80"))
C --> D(("70"))
D --> E(("60"))
E --> F(("50"))
F --> G(("40"))
G --> H(("30"))
H --> I(("20"))
- Zeichne den AVL der Entsteht, wenn dieselben Werte in einen AVL Baum eingefügt werden.
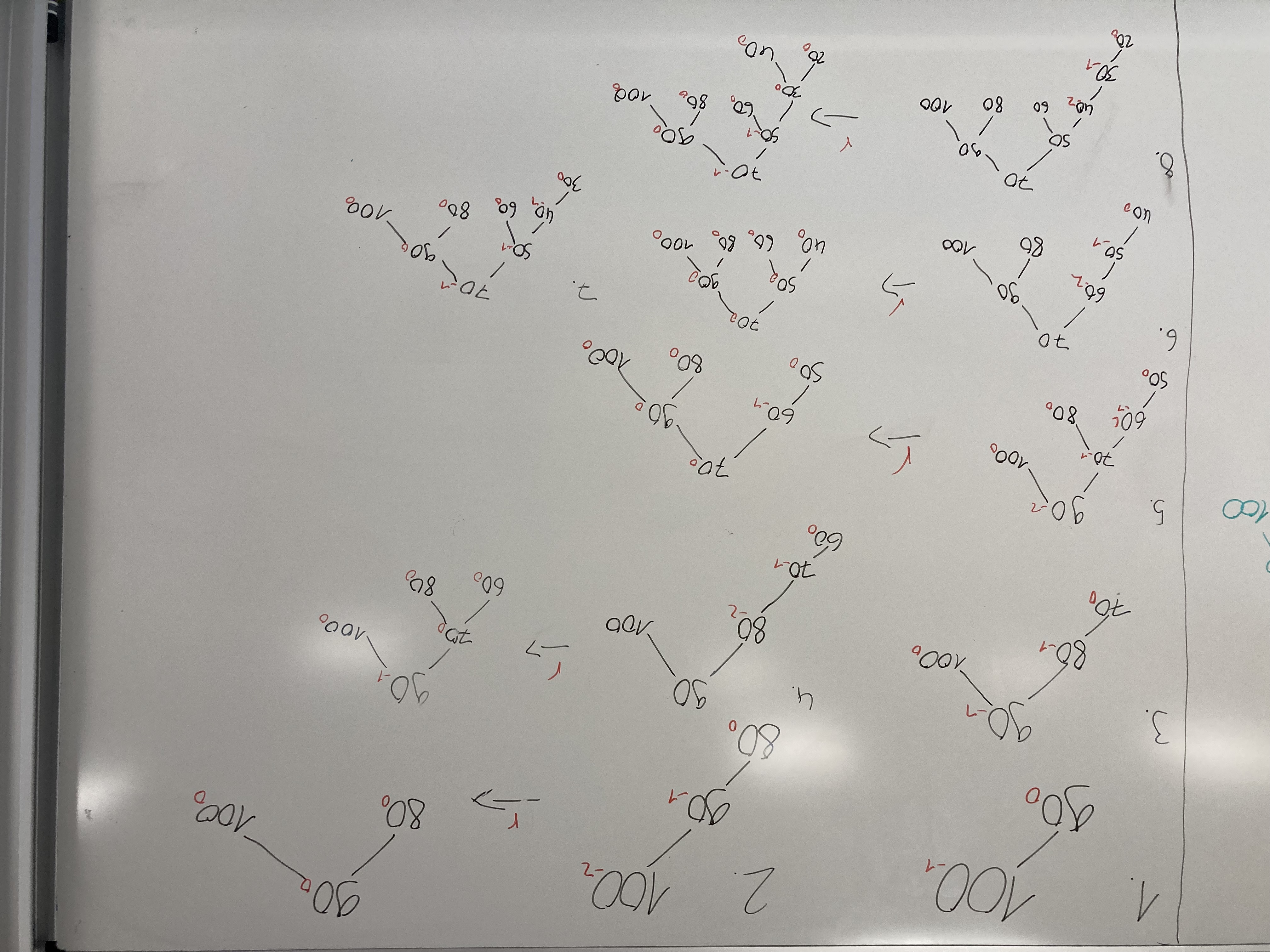
- Überlegt euch eine Zahlenfolge mit der alle Rotation abgedeckt werden. Bereite dich darauf vor, den Vorgehen zu erläutern.

